Haskell は関数型言語ですから、関数が主役だろうという想像ができます。まさ にそのとおりです。この節では Haskell における関数の貌をいくつか見てい きます。
先ず、ふたつの引数を足す関数の定義を考えましょう。
add :: Integer -> Integer -> Integer
add x y = x + y
これは、カリー化(curry)された関数の一例です。(「カリー
」という呼び名はこの概念を有名にした、Haskell Curry から来ています。
アンカリー化(uncurry)された関数をえるには、タプルを使います。
add (x,y) = x + y
しかし、こうしてしまうと、この add は1引数の関数になってしまい
ます。) 関数 add の適用は add e1
e2 という形式になります。これは、
(add e1) e2 と同等の式
です。なぜかというと関数適用は左結合性をもつからです。いいかえ
れば、関数 add を最初の引数に適用すると、新しい関数ができて、こ
れをふたつめの引数に適用するということです。このことは、関数
add の型 Integer->Integer->Integer とも整合がと
れています。この型は、Integer->(Integer->Integer) と同等
のものです。ここで、 -> は右結合性をもっています。
実際この add を使うと前とはちがうやり方で inc を定義す
ることができます。
inc = add 1
この例は、カリー化された関数の部分適用 (partial
application) の一例であり、関数が返りの値となる例のひとつです。
今度は関数を引数としてわたす例を考えてみましょう。よくしられた
map 関数が完璧な例です。
map :: (a->b) -> [a] -> [b]
map f [] = []
map f (x:xs) = f x : map f xs
[関数適用はどんな中置演算子よりも高い優先順位をもっています。そのため、2
つめの等式の右辺は (f x) : (map f xs)
のように構文解析されます。] この map 関数は多相型であり、その型
は、最初の引数が関数であることを明示しています。さらに、2つの a
は同じ型にインスタンス化されなければならないことに注意してください。
( b についても同じです。) map の使用例をみると、リスト
の要素をそれぞれ1だけ増加させることができます。
map (add 1) [1,2,3] => [2,3,4]
これらの例は関数が第一級の対象であることを示しています。このような使いか たをする関数はふつう高階 (higher-order) 関数とよばれます。
等式を使わずにラムダ抽象 (lambda abstraction) を使って無
名関数を定義することができます。たとえば、inc と同等の関数は
\x -> x+1 と書く
ことができます。同様に、add と同等の関数は
\x -> \y -> x+y と書けます。入れ子に
なったラムダ抽象は簡略化して、\x y -> x+y と
書いても同じことです。そして、
inc x = x+1
add x y = x+y
という等式は、
inc = \x -> x+1
add = \x y -> x+y
という等式を簡略化して書いたものと同等ということです。この同等性について
はこれから説明します。
一般に x があって、その型が t1 で、exp の型 が t2 である場合、\x->exp の型は t1->t2 ということになります。
中置演算子は関数なので、等式を使って定義することができます。たとえば、リ
ストの連結演算子を定義すると、このようになります。
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs++ys)
[中置演算子の字句は、すべて「記号」で構成されます。これは、英数字で
構成される一般の識別子とは対照的です ( §2.3 )。
Haskell にはマイナス( - )をのぞき前置演算子はありません。マイナ
ス( - )は前置演算子にも、中置演算子にもなります。]
もうひとつ、関数上の重要な中置演算子、関数合成( function
composition )の例を見てみましょう。
(.) :: (b->c) -> (a->b) -> (a->c)
f . g = \ x -> f (g x)
中置演算子はまさに関数ですから、関数と同じように、部分適用が可能です。 Haskell では中置演算子の部分適用のことをセクション ( section )といいます。例を見ましょう。
| (x+) | = | \y -> x+y |
| (+y) | = | \x -> x+y |
| (+) | = | \x y -> x+y |
[ここでの括弧は必須です。]
上の例の最後のセクションの形式は中置演算子から同等の関数値へ変換する働き
をします。この形式は中置演算子を関数の引数として渡すときに便利な方法です。
たとえば、map (+) [1,2,3] のようにします。(読者の皆さ
んはここで、関数のリストが返されていることを確かめてください。) 関数の型
を与える際にも必要になります。これはすでに (++) および
(.) の例で示しましたね。さて、これですでに定義した add
が (+)、inc が (+1) で定義できることがわかり
ます。実際これらの定義がすっきりします。
inc = (+ 1)
add = (+)
中置演算子を関数値に変換できましたが、それでは、その逆は可能なのでしょう か。可能です。関数値をバッククウォートで括るだけです。たとえば、 x `add` y は、add x y と同じです。 (これは、add がバッククオート で括るのであって、文字の 場合のアポストロフィ(あるいはシングルクウォート)で括る わけではありません。つまり、'f' は文字で、`f` は中置演 算子です。幸い、ほとんどの ASCII 端末ではこのふたつを区別できるようになっ ています。(手で書くとそうはいかないようです。) 関数によっては、中置演算 子にしたほうが読みやすくなります。たとえば、リストの要素かどうかを調べる 述語関数 elem がその例です。x `elem` xs は直 観的に「x が属しているのは xs である。( x is an element of xs )」と読めます。
[前置/中置演算子 - のセクションについてはいくつかの特別なルール があります。(§3.5,§3.4)。]
ここまでで、読者のみなさんは関数の定義のしかたにいろいろあって、混乱した かもしれません。これらの定義のメカニズムのサポートを決定するにあたっては、 歴史的な慣習も部分的には反映されていますし、一貫性を確保したい(たとえば、 中置演算子と普通の関数の取り扱いなど)という要望も反映されています。
結合性宣言( fixity declaration ) はすべての中置演算子と
中置構築子 ( `elem` のような一般の識別子に由来するものも含む)に
対しておこなうことができます。この宣言では 0 から 9 までの優先レベル( 9
が最強です。一般の関数適用の優先レベルは 10 と仮定されています。)と、右
結合性、左結合性をもつ、あるいは結合性をもたない、という指定をします。例
をあげると ++ と . の結合性宣言は、
infixr 5 ++
infixr 9 .
です。両方とも右結合性が指定されています。++ は優先レベル 5
で . は優先レベル 9 と指定されています。左結合性は
infixl を使って指定し、結合性のないことは infix で指定
します。おなじ結合性宣言で 1 つ以上の演算子の結合性について指定できます。
もし、ある演算子に対して、結合性宣言をしない場合はデフォルトで
infixl 9 が指定されたことになります。( 結合性ルールの定義
の詳細については §5.6
参照のこと。)
bot が次のように定義されているとしましょう。
bot = bot
bot は停止しない式です。このような停止しない式の値を抽
象的に _|_(ボトムと読む)と表わします。ある種の実行時エラーになる式、たと
えば、1/0 のような式もこの値を持ちます。このようなエラーは回復
不可能で、プログラムはこれ以上継続することはできなくなります。I/O システ
ムのエラー(たとえば、EOF エラーなど)は回復可能で、べつの方法で取り扱い
ます。(このような I/O エラーは、実はエラーではなく、例外です。例外につい
ての詳細は 7 節でふれます。)
関数 f が正格 ( strict ) であるとは、停止しない
式に適用されれば、その適用式も停止しないことをいいます。いいかえると、
f bot が _|_ の時でかつその時にかぎり、f は正格で
あるといいます。ほとんどのプログラミング言語では、すべての関数
が正格です。ただ、 Haskell では違います。簡単な例、つねに 1 を返す関数
const1 を考えましょう。定義は、
const1 x = 1
です。const1 bot の値は Haskell では 1 です。操作
的な観点からいうと、const1 はその引数の値を「必要」としないので、
引数は決して評価されません。だから停止しない計算に陥いることがないのです。
こういうわけで、非正格関数は「遅延関数 ( lazy function ) 」とも呼ばれ、
その引数の評価については「遅延評価」とか「必要呼び評価」とかいわれていま
す。
Haskell では、エラーや停止しない値は、意味論的に同じものですから、上の引数 にはエラーも含まれています。たとえば、 const1 (1/0) もちゃ んと評価されて 1 になります。
非正格関数は多くの場面で、たいへん役に立ちます。そのなかで、主要な利点は、 プログラマが評価の順に気をくばらなくてもよい、ということです。計算上高価 な値を、必要もないのに余分な計算をしなければならないかもしれない、などと 心配せずに関数へ渡すことができます。重要な例のひとつは、無限の ( infinite ) データ構造です。
もうひとつ別のやりかたで非正格関数を説明しましょう。Haskell は伝統的な言
語のように代入 ( assignment ) ではなく、定義
( definition ) を用いて計算をすすめます。たとえば、
v = 1/0
のような宣言は、「 v を 1/0 と定義する」と読みます。こ
れは、「 1/0 を計算し、その結果を v へ格納する」とは読
みません。v の値(定義)が必要になったときにのみゼロ除算エラーが
発生します。宣言それだけでは計算は起こりません。代入を必要とするプロ
グラミングではその代入の順序に細心の注意をはらう必要があります。プログラ
ムの意味は代入がおこる順序に依存します。一方、定義はずっと単純で、プログ
ラムの意味には影響あたえず、どのような順で出現してもかまいません。
Haskell の非正格な性質の利点のひとつは、データコンストラクタもが非正格で あることです。このことはべつに驚くべきことではありません。コンストラクタ は特殊な関数にすぎません(ふつうの関数との違いは、パターンマッチで使われ るということです)。たとえば、リストの構築子、: は非正格です。
非正格の構築子で(概念的に)無限の( infinite )データ構造を
定義することができます。これは、1 の無限リストです。
ones = 1 : ones
さらに面白いのは、numsFrom 関数です。
numsFrom n = n : numsFrom (n+1)
numsFrom n は n から始まる無限の整数リストです。
これを使って、平方数の無限リストを構成することができます。
squares = map (^2) (numsFrom 0)
(ここで、セクションの使いかたに注目してください。^ は中置の指数
演算子です。)
当然のことながら、実際の計算では、そこから、有限の部分を取り出したいわけ です。Haskell ではこの用途で使える関数があらかじめたくさん定義されていま す。take、takeWhile、filter 等々です。Haskell の定義には多くの組み込みの関数や型が含まれています。これらを「標準プレリュー ド( Standard Prelude )」と呼びます。標準プレリュード全体は、Haskell Report の付録 A にあります。リスト上の数多くの有用な関数が PreludeList の部分にありますので、参照してください。例をあげま しょう。take はリストから最初の n 個の要素を取り出しま す。
take 5 squares => [0,1,4,9,16]
上にあげた、ones の定義は、循環リスト( circular list )の例です。ほとんどの場合、遅延性は効率の面で非常に重要です。表 現が本当の循環リストとして実装されるので、空間が節約できます。
循環性を使用した別の例をみてみましょう。フィボナッチ数列はつぎのような循
環数列をつかって効率よく計算することができます。
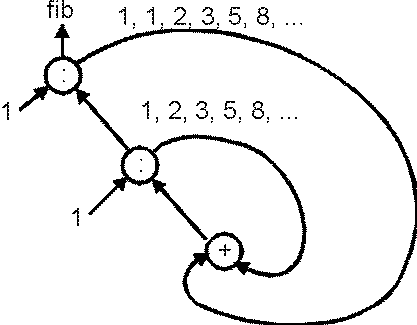
fib = 1 : 1 : [ a+b | (a,b) <- zip fib (tail fib) ]
ここで、zip は標準プレリュードにある関数で、引数のふたつのリス
トの要素を互いにペアにしたリストを返す関数です。
zip (x:xs) (y:ys) = (x,y) : zip xs ys
zip xs ys = []
無限リスト fib が自分自身をつかってどのように定義されているかに
注目してください。「自分の尻尾をおいかける」ような定義になっていますね。
実際、この計算を絵にえがくと図 1 のようになります。

無限リストの応用のさらにもうひとつの例については 4.4 節を参照のこと
Haskell には error という組み込みの関数があります。この関数の型 は String->a です。これはすこしばかり奇妙な関数です。型から すると、この関数の返す値の型は多相の型で実際の型がわかりません。この型の 引数を受けとるわけではないからです。
すべての型によって「共有」される値 _|_ というのが存在します。
実際、意味論的には、error の返す値は常にこの値です(すべてのエラー
の値は _|_ であることを思い出してください)。しかし、実装はチェックのため
の error の文字列引数を印字するというのが妥当なところでしょう。
それで、この関数は、なにか「誤りがあった場合」、プログラムを停止させたい
ときに便利です。たとえば、標準プレリュードでは、head の定義は以
下のようになっています。
head (x:xs) = x
head [] = error "head{PreludeList}: head []"