やさしい Haskell 入門 ( Version 98 )
back
next
top
パターン照合の例は前に length や fringe の関数の 定義の際に示しました。この節ではパターン照合のプロセスを詳細に見て いきましょう( §3.17 ) ( Haskell におけるパターン照合は、たとえば Prolog のような、論理 プログラミング言語にみられるものとは違いがあります。とくに、Haskell の 照合は「一方向」です。一方 Prolog の照合は(単一化による)「双方向」で、 その評価機構のなかで暗黙のバックトラックによるもです。)
パターンは「第一級の対象」ではありません。いろいろな種類のパターンの固定
的な集合があるだけです。すでに、データ構築子のパターンのいくつ
かの例をしめしました。以前に定義した length と fringe
はこうしたパターンをつかって定義してあります。前者は「組み込み」の型(リ
スト)の上での例で、後者は、「ユーザ定義」の型( Tree )の上での例
です。照合はユーザ定義かどうかには関係なく、すべての型で使うことが
できます。これには、タプル、文字列、数、文字などが含まれます。例をあげま
しょう。ここに、「定数」のタプルに対して照合が成功する contrived 関
数があります。
contrived :: ([a], Char, (Int, Float), String, Bool) -> Bool
contrived ([], 'b', (1, 2.0), "hi", True) = False
この例で、入れ子になったパターン(入れ子の深さは任意)も使えるこ
とがわかります。
テクニカルないいまわしをすれば、仮引数( formal parameters ) (レポートでは変数( variable )と呼ばれて いるもの)もパターンです。つまり、ある値にかならず照合が成功します。 この照合が成功する副作用として、仮引数は照合が成功した値に束縛されます。その わけは、ひとつの等式であれば、そのなかのパターンには、2つ以上の同じ仮引 数が含まれてはいけないからです。(これは、線型性 ( linearity ) とよばれている性質です。§3.17、§3.3、§4.4.2)
仮引数のような必ず照合が成功するようなパターンのことを不可反駁 ( irrefutable )パターンといいます。反対に可反駁 ( refutable )パターンは照合が成功しない可能性があります。上であげた contrived の例はこの可反駁パターンの例です。不可反駁パターンに は 3 つの種類があります。そのうち 2 つを紹介しましょう。(のこりは、4.4 節までまってください。)
場合によってはパターンに名前がついていれば、等式の右辺で使えて便利なこと
があります。たとえば、リストの第一要素を複製する関数はつぎのように書けま
す。
f (x:xs) = x:x:xs
(「:」は右結合性があることを思いだしてください。) x:xs
というパターンが左辺と右辺の両方にあります。可読性向上のためには
x:xs は一度だけ書くほうがよく、アズパターン
( as-pattern )を使ってこれを達成します。(このパターンを使うもうひ
とつの利点は、素朴な実装では、照合が成功した値を再利用せずに、x:xs
を再構築することになるからです。)
f s@(x:xs) = x:s
技術的な観点からいうと、アズパターンは照合に常に成功します。ただし、
サブパターン(この場合は、x:xs )はもちろん照合が成功しないこともあり
ます。
よくある状況をもうひとつ、それはとくに値を気にしない照合です。たと
えば、2.1 節で定義した
head 関数や tail 関数は次のように書き換ることができま
す。
head (x:_) = x
tail (_:xs) = xs
この定義では、入力されたものの一部は気にしないということがはっきり「広告」
されています。各ワイルドカードはそれぞれ独立にどんなものとも照合が成功しま
す。しかし、仮引数の場合とちがい、それぞれは何にも束縛されません。というわ
けで、ワイルドカードパターンはひとつの等式のなかに 1 つ以上あってもかま
いません。
これまで、個々のパターンがどのように照合に成功し、あるいは可反駁のものと、 不可反駁のものがあるということを議論してきました。しかし、どのようにして、 その処理全体がおこなわれるのでしょうか。どのような順序で照合がためされる のでしょうか。もし、どのパターンも成功しなかったらどうなるのでしょうか。 この節ではこのことについて考えていきましょう。
パターン照合は失敗する( fail )こともあるし、成 功する( succeed )こともあるし、あるいは発散する ( diverge )こともあります。成功した照合が、そのパターン中の仮引数 を束縛します。発散は、パターンが必要とした値がエラー( _|_ )を含んでいた 場合に起こります。照合の処理自体は「上から下へ、左から右へ」おこな われます。ひとつの等式のなかのどこでパターン照合が失敗しても、その等式 全体に対するパターン照合が失敗したことになり、次の等式が試されます。す べての等式でパターン照合が失敗すると、その関数適用の値は _|_ になり、 実行時エラーとなります。
たとえば、[1,2] を [0,bot] に照合させようとすると、 1 は 0 と照合しませんので、この照合は失敗しま す。(以前に定義した bot は _|_ に束縛されていることを思い出して ください。) しかし、もし、[1,2] を [bot,0] にマッチさ せようとすると、1 を bot へ照合させる際に発散がおこ ります。
パターン照合のルールで唯一ひねくれているところは、トップレベルのパ
ターンがブーリアンガード部をもつこともあるということです。数の
符号を抽象化する関数の例をみると、
sign x | x > 0 = 1
| x == 0 = 0
| x < 0 = -1
のようになります。ここで注意すべきは一連のガードが同じパターンを使ってい
るということです。これらは上から下へ評価され、最初に True となっ
たところで照合が成功します。
パターン照合のルールが、関数の意味に微妙に影響することがある。たと
えば、つぎの take の定義
take 0 _ = []
take _ [] = []
take n (x:xs) = x : take (n-1) xs
と、これとはちょっとだけちがう定義(最初の 2 つの等式の順序が逆のもの)
take1 _ [] = []
take1 0 _ = []
take1 n (x:xs) = x : take1 (n-1) xs
を考えてみましょう。次の結果に注目してください。
| take 0 bot | => | [] |
| take1 0 bot | => | _|_ |
| take bot [] | => | _|_ |
| take1 bot [] | => | [] |
takeは 2 番目の引数により重きをおいて定義され、一方、 take1 は 1 番目の引数により重きをおいて定義されていることがわか ります。この場合、どちらがよい定義であるかはむずかしいところです。ただ、 実際の応用の場面では、意味の違いをひきおこすことがあるということを覚えて おいてください。 (標準プレリュードでは take の方の定義を採用し ています。)
パターン照合を使うと値の構造的な性質に基づいた「ディスパッチ制御」 をすることができます。しかしながら、多くの状況では、これを実現する必要が あるたびに関数を定義するなどということはやりたくはありません。 しかし、これまでは、どのように関数定義のなかでパターン照合をおこなうか を示しただけでした。Haskell の case 式( case expression )はこの問題を解決してくれます。関数定義のなかでのパターン照合の意味は、 実は case 式のより単純なものと考えられることが Haskell レポートに示され ています。次のような関数定義の形式を考えます。
| f p11 ... p1k = e1 |
| ... |
| f pn1 ... pnk = en |
ここで、各 pij はパターンです。この定義は意味論 的には以下のものと同等です。
f x1 x2 ... xk = case (x1, ..., xk) of
| (p11, ..., p1k) -> e1 |
| ... |
| (pn1, ..., pnk) -> en |
ここで xi は新しい識別子です。(ガードを含む、より一般的な解釈に
ついては §4.4.2 を参照のこ
と) 例をしめすと、まえにあげた take の定義は以下と同等です。
take m ys = case (m,ys) of
(0,_) -> []
(_,[]) -> []
(n,x:xs) -> x : take (n-1) xs
型の正当性について以前には言及しませんでしたが、case 式の右辺あるいは一 連の関数定義を含む等式の右辺はすべて同じ型でなければなりません。より正確 にはそれらはすべて同じ主型を共有しなければなりません。
case 式のパターン照合のルールは関数定義でのパターン照合のルー ルとおなじです。それゆえ、ここで新しく学習することはなにもないのですが、 case 式の利便性については注目してください。case 式のよく知られている特殊 構文があります。それは 条件式( conditional expression ) です。Haskell では条件式はおなじみの形式をもちます。
if e1 then e2 else e3
これは以下の構文の簡略形です。
| case e1 of | True -> e2 |
| False -> e3 |
この展開を見ると e1 が Bool 型でなければならず、 e2 や e3 は同じ型(とはいえこちらは任意の型)でなけ ればならないことがはっきりとわかります。いいかえれば、 if_then_else_ は関数であると見なせば、 Bool->a->a->a という型をもっているといえます。
Haskell ではもうひとつ別のパターンが許されています。それは遅延パター ン( lazy pattern )とよばれるもので、~pat という形式 をとります。遅延パターンは不可反駁で、値 v の ~pat に 対する照合は pat が何であっても常に成功します。操作論の観点からいう と pat のなかの識別子が右辺で「利用」されるとすると、それは v が pat に マッチすると仮定した場合の値に束縛されるか、さもなければ、_|_ となります。
遅延パターンは無限のデータ構造が再帰的に定義されているような場合に便利で す。例をあげましょう。無限リストはシミュレーションプログラムを 書くのに大変つかいよいデータ構造です。こうした使い方をする無限リストを よくストリームといいます。サーバプロセス server と ク ライアントプロセス client との間のやりとりの簡単なケースを考え てみましょう。client は一連の要求を server に 送り、server はおのおのの要求に対して、ある種の応答を 返します。この状況をフィボナッチの例でやったように絵であらわすと、図 2 のようになります。( client は引数として初期メッセージもとること に注意してください。)
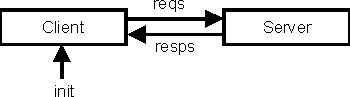
ストリームを使ってこのメッセージシーケンスをシミュレートすると、Haskell
のコードでは、
reqs = client init resps
resps = server reqs
のようになります。これらの等式は上の図式をそのままコードに移しかえたもの
です。
さらに、サーバとクライアントの構造がどのようなものか、以下のように仮定し
ましょう。
client init (resp:resps) = init : client (next resp) resps
server (req:reqs) = process req : server reqs
ここで、next はサーバからの応答を与えられて、次の要求を決定する
関数であり、process はクライアントからの要求を与えられて、それ
にあった応答を返す関数であるとします。
残念ながら、このプログラムには大きな問題があります。このプログラムはなに
も出力しないのです。問題は、client が reqs と
resps の再帰的な設定のなかで使われているので、最初の要求を送信
する前に応答リストと照合を試みようとすることなのです。つまり、パター
ン照合がおこなわれるのが「早すぎる」のです。これを是正するひとつの
方法は以下のように client を再定義することです。
client init resps = init : client (next (head resps)) (tail resps)
これで動作するようになりますが、この解決法は、その前の定義とおなじには読
めません。もっとよい解決法は遅延パターンを使う方法です。
client init ~(resp:resps) = init : client (next resp) resps
遅延パターンは不可反駁なので、照合はただちに成功し、そのおかげで最
初の要求が発信され、それから最初の応答が生成されます。これでエンジンが給
油ずみになり、のこりは再帰の部分が面倒をみてくれます。
この例は、以下のように定義を加えれば、実際に動作します。
init = 0
next resp = resp
process req = req+1
実際に動作させてみると、
take 10 reqs => [0,1,2,3,4,5,6,7,8,9]
のようになります。もうひとつの遅延パターンの例として、以前に定義したフィ
ボナッチ数列を考えてみましょう。
fib = 1 : 1 : [ a+b | (a,b) <- zip fib (tail fib) ]
これを、アズパターンを使って書換えるとすると
fib@(1:tfib) = 1 : 1 : [ a+b | (a,b) <- zip fib tfib ]
このバージョンの fib の利点(小さいですが)は、左辺の
tfib で展開した形式を使用できるので、 tail を右辺で使
わなくてよいということです。
[この種の等式はパターン束縛( pattern binding )とよばれま す。その理由は、トップレベルにある等式で左辺全体がひとつのパターンになっ ているからです。すなわち、fib と tfib はともに宣言内で 束縛されているということです。]
さて、以前と同じ論法でいうとこのプログラムはなんの出力もないということを 導くことができそうです。しかし、奇妙なことにこのプログラムは出力が生 成されます。その理由は簡単です。Haskell ではパターン束縛は暗黙のう ちに ~ がパターンの前についているものとみなすからです。このことは、 パターン束縛に期待される共通のふるまいのほとんどを反映しています。ある種 の変則的な状況はこのチュートリアルの守備範囲を越えるので、ここでは説明し ません。このようにして、Haskell の遅延パターンは暗黙のうちに重要な役割を はたすことが理解できます。
ひとつの式のなかで入れ子の有効範囲をつくりたいことがよくあります。これは、 その部分だけの局所的な束縛をつくりたいときです。ある種の「ブロック構造」 の形式が欲しくなります。Haskell ではこれを実現するのに 2 つの方法が用意 されています。
Haskell のlet 式( let expression )は入れ子になった束縛の
集まりが必要なときに役に立ちます。簡単な例を考えてみましょう。
let y = a*b
f x = (x+y)/y
in f c + f d
let 式によってつくられる束縛の集りは、相互再帰的
( mutually recursive )で、パターン束縛は遅延パターンとして扱われ
ます( ~が暗黙のうちについているということです)。ここで許される
宣言は、型シグネチャー、関数束縛、パターン束縛
のみです。
ときには、いくつかのガードをもつ等式にまたがる有効範囲束縛があれば便利な
こともあります。そんなときには where 節( where clause )
が必要です。
f x y | y>z = ...
| y==z = ...
| y<z = ...
where z = x*x
これは、let 式と同じようには使えないことに注意してください。
where 節はそれが覆う式の上にしか有効範囲がありません。
where 節は等式の集まりあるいは case 式のトップレベルでしか認め
られていません。また、let 式での束縛の性質と制約が
where 節の束縛にも適用されます。
入れ子の有効範囲のこれら 2 つの形式は非常によく似たものですが、 let 式はひとつの式であり、一方、where 節は 式ではないということを覚えてください。where 節は関数宣 言および case 式の構文の一部です。
読者のなかには、なぜ Haskell ではセミコロンあるいはそれにかわる終端記号
を使わずにすんでいるのか不思議におもった方もいるでしょう。これらの記号は
等式や宣言などの終端を示すものですが、それがなぜ必要ないのでしょうか。例
をあげましょう。前の節の let 式を考えてみましょう。
let y = a*b
f x = (x+y)/y
in f c + f d
構文解析はなぜ次のように解析したりしないのでしょうか。
let y = a*b f
x = (x+y)/y
in f c + f d
答えは、Haskell はレイアウト( layout )と呼ばれる、二次元 構文を用いているからです。レイアウトは「カラム位置にならべられた」宣言に 依存しています。上の例で、y と f とは同一のカラム位置 からはじまっていることに注目してください。レイアウトのルールの詳細は Haskell レポート(§1.5,§B.3)の方にまかせますが、 実用上はこのレイアウトの使い方は直観的にわかります。ただ、覚えておいてほ しいことがふたつあります。
まず第一は、キーワード where、let, あるいは of につづく次の文字は、それぞれ、where 節、let 式、case 式のな かの宣言のはじまるカラム位置を決定するものであることです。(このルールは、 クラス宣言やインスタンス宣言のなかの where にも適用されます。こ れについては 5 節を参照して ください。) これにより、宣言部はキーワードと同じ行でも、次の行ででもはじ めることができます。( do キーワード、これについては後で議論しま すが、これもレイアウトを使います。)
ふたつめは、開始カラムは直接囲われている節の開始カラムよりも右になければ ならないということです。(そうしなければ、曖昧になってしまいます。) 宣言 の「終端」は束縛形式の開始カラムの位置あるいはそれよりも左側でなにかが開 始されたときに起こります。( Haskell では慣習として、タブは 8 個のスペー スとして見なします。なので、エディタで 8 カラムタブ以外の表示を使ってい る場合には注意が必要です。)
レイアウトは実際には明示的なグルーピング機構の簡略表記です。あ
る種の状況ではグルーピング機構は大変役に立つので、これについては言及する
価値があります。上の let の例は以下のものと同等です。
let { y = a*b
; f x = (x+y)/y
}
in f c + f d
明示的な波括弧とセミコロンに注目してください。この明示的な表記方が便利な
のは、ふたつ以上の宣言を 1 行におさめたいときです。たとえば、以下は正し
い式です。
let y = a*b; z = a/b
f x = (x+y)/z
in f c + f d
もうひとつのレイアウトを明示的な区切り子に展開する例については §1.5 を参照してく
ださい。
レイアウトを利用すれば、宣言リストが構文的にごしゃごしゃするのが少なくな り、可読性がまします。使いかたを覚えるのは簡単ですので、どしどし使ってく ださい。